在公務(wù)員考試行測數學(xué)運算中,有一類(lèi)植樹(shù)問(wèn)題,這類(lèi)題目沒(méi)有什么解題技巧,而是利用對應的公式就可以很容易的解答,那么,接下來(lái)江蘇公務(wù)員考試網(wǎng)就幫考生總結一下植樹(shù)問(wèn)題所用到的公式以及怎么應用。
一、植樹(shù)問(wèn)題的類(lèi)型和應對公式
例如:在一周長(cháng)為100米的湖邊種樹(shù),如果每隔5米種一棵,共要種多少棵樹(shù)?這樣在一條“路”上等距離植樹(shù)就是植樹(shù)問(wèn)題。在植樹(shù)問(wèn)題中,“路”被分為等距離的幾段,段數=總路長(cháng)÷間距、總路長(cháng)=間距×段數。
根據植樹(shù)路線(xiàn)的不同以及路的兩端是否植樹(shù),段數與植樹(shù)的棵數的關(guān)系式也不同,下面就從不封閉路線(xiàn)的植樹(shù)和封閉路線(xiàn)植樹(shù)來(lái)一一說(shuō)明。
(1)不封閉植樹(shù):指在不封閉的直線(xiàn)或曲線(xiàn)上植樹(shù),根據端點(diǎn)是否植樹(shù),還可細分為以下三種情況:
①兩端都植樹(shù):兩個(gè)端點(diǎn)都植樹(shù),樹(shù)有6棵,段數為5段,即有植樹(shù)的棵數=段數+1,結合段數=總路長(cháng)÷間距,則:棵數=總路長(cháng)÷間距+1,總路長(cháng)=(棵數-1)×間距。
②兩端都不植樹(shù):兩個(gè)端點(diǎn)都不植樹(shù),可知植樹(shù)的棵數=段數-1,結合段數=總路長(cháng)÷間距,則:棵數=總路長(cháng)÷間距-1,總路長(cháng)=(棵樹(shù)+1)×間距。
③只有一端植樹(shù):只有一個(gè)端點(diǎn)植樹(shù),可知植樹(shù)的棵數=段數,結合段數=總路長(cháng)÷間距,則:棵數=總路長(cháng)÷間距,總路長(cháng)=棵數×間距。
(2)封閉植樹(shù):指在圓、正方形、長(cháng)方形、閉合曲線(xiàn)等上面植樹(shù),因為頭尾兩端重合在一起,所以種樹(shù)的棵數等于分成的段數。所以棵數=總路長(cháng)÷間距,總路長(cháng)=棵數×間距。
二、兩邊植樹(shù)問(wèn)題
除了在路的一邊植樹(shù)外,還有路的兩邊都植樹(shù)的情況,這時(shí)就要先判斷出植樹(shù)類(lèi)型,計算出一邊植樹(shù)的情況,再根據一邊求兩邊情況。
【例題1】如果每500米遠架一根電線(xiàn)桿,則30公里需要架設多少根電線(xiàn)桿?
A.31 B.30 C.61 D.60
解析:此題答案為C。共需要架設30×1000÷500+1=61根電線(xiàn)桿。
三、不同間隔植樹(shù)問(wèn)題
在一些植樹(shù)問(wèn)題中,往往存在兩種或多種植樹(shù)方式。這種情況下,就會(huì )出現重復植樹(shù)問(wèn)題,常需要結合最小公倍數找出重合點(diǎn)。
【例題2】某工地從一條直道的一端到另一端每隔3米打一個(gè)木樁,一共打了49個(gè)木樁。現在要改成4米打一個(gè)木樁,那么可以不拔出的木樁共有多少個(gè)?
A.8 B.9 C.11 D.13
解析:此題答案為D。每隔3米打一木樁對應每隔3米植樹(shù),兩端都打對應兩端都植樹(shù),因此直道的總長(cháng)=段數×間距=(棵數-1)×間距=(49-1)×3=144米。
依題意,不拔出來(lái)的木樁距離起點(diǎn)的距離必須能被3和4整除,3和4的最小公倍數是12,即從起點(diǎn)開(kāi)始每隔12米有一個(gè)木樁可以不拔出,144÷12=12,故有12+1=13根木樁不用拔出。
四、植樹(shù)問(wèn)題變形
在數學(xué)運算中還有一些變形題,如鋸木頭、走樓梯等實(shí)際問(wèn)題,這些變形只是形式上的改變,其本質(zhì)仍然是植樹(shù)問(wèn)題。中公教育專(zhuān)家發(fā)現,在最近幾年的行測考試中,植樹(shù)問(wèn)題往往以這種變形題出現。
解決植樹(shù)問(wèn)題的變形題,要注意端點(diǎn)是否“植樹(shù)”,分清“棵數”與“段數”之間是+1還是-1。
常見(jiàn)的變形題:鋸木頭、爬樓梯、重合、隊列問(wèn)題均可視為兩端都不植樹(shù)問(wèn)題,其中的知識要點(diǎn)如下:
鋸木頭:要鋸成n段,則需鋸(n-1)次;
爬樓梯:從1層到n層,需爬(n-1)段樓梯;若每爬完一段,休息一次,則需休息(n-2)次;
重合問(wèn)題:n段接在一起,重合的有n-1段;
隊列問(wèn)題:有n個(gè)人(或n輛車(chē)),中間有n-1個(gè)空。
【例題3】把一根鋼管鋸成小段,一共花了28分鐘。已知每鋸開(kāi)一段需要4分鐘,這根鋼管被鋸成了多少段?
A.3 B.4 C.6 D.8
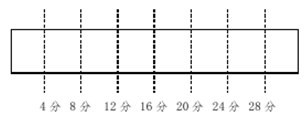
解析:此題答案為D。要求鋼管被鋸的段數,必須首先求出鋼管被鋸開(kāi)幾處。
從上圖我們可以看出鋼管有28÷4=7處被鋸開(kāi),因而鋸開(kāi)的段數有7+1=8段。題中被鋸開(kāi)的地方即植樹(shù)位置,因此問(wèn)題相當于“兩端都不植樹(shù)”問(wèn)題,棵數=段數-1。
上面幾道例題基本套用公式,分清楚類(lèi)型就可以迅速作答了。希望可以幫助考生把植樹(shù)問(wèn)題的解題思路理清,以后再碰到這類(lèi)問(wèn)題就不會(huì )再花費大量的時(shí)間了。
行測更多解題思路和解題技巧,可參看2015年公務(wù)員考試技巧手冊。










