求幾個(gè)數的最大公約數,除了我們熟知的短除法和分解質(zhì)因數法之外,還有《幾何原本》中記載的“輾轉相除法”,這種算法在我國則要追溯到《九章算術(shù)》中記載的“更相減損術(shù)”。經(jīng)過(guò)分析分解質(zhì)因數法(短除法原理相同)和更相減損術(shù)(輾轉相除法原理相同)的原理,查閱資料,總結上述兩種方法的特點(diǎn)及優(yōu)缺點(diǎn),在此為江蘇公務(wù)員考試網(wǎng)(www.jsgwy.com.cn)大家介紹一種求“最小公倍數”和“最大公約數”的新方法——“消減法”。
一、 “消減法”介紹
眾所周知,任何兩個(gè)不相等的數的和或差里一定含有這兩個(gè)數的公約數,為了方便,我就采用兩個(gè)數的差與其中一個(gè)數相互約分的方式,消去這兩個(gè)數的公約數,從而求得最大公約數和最小公倍數。
“消減法”具體求法是這樣的:用其中一個(gè)數作分子,這兩個(gè)數的差作分母,再把它化成最簡(jiǎn)分數。把最簡(jiǎn)分數的分子與另一個(gè)數(不是原來(lái)作分子的那個(gè)數)相乘,所得的乘積就是這兩個(gè)數的最小公倍數;拿原分母(原來(lái)兩個(gè)數的差)除以最簡(jiǎn)分數的分母,得到的商就是這兩個(gè)數的最大公約數。
比如:求18和30的最小公倍數和最大公約數。
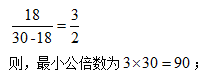
“消減法”同樣也適用于求三個(gè)數的最小公倍數和最大公約數,方法如下:
(1)求最小公倍數:

更多解題思路和解題技巧,可參看2018年公務(wù)員考試技巧手冊










