對于行程問(wèn)題很多人其實(shí)并不陌生,其實(shí)就是一個(gè)人或者幾個(gè)人按照一定的速度開(kāi)展一段旅途;旅途中大家會(huì )相遇、會(huì )追及。這是行程問(wèn)題的基本考查方法,考生在備考的時(shí)候區分起來(lái)也很好區分。然而在實(shí)際公職考試的過(guò)程中,還有一些其他考法,比如當旅客變成牛和草,旅途轉移到了草場(chǎng),這就是今天要講解的一種小題型——牛吃草問(wèn)題。
接下來(lái)讓我們通過(guò)一道例題來(lái)體會(huì )一下當行程遇上牛和草又會(huì )發(fā)生哪些神奇的變化。
例1:牧場(chǎng)上有一片青草,每天都勻速生長(cháng)。這片青草供給10頭牛吃,可以吃12天;或者供給15頭牛吃,可以吃6天。如果供給20頭牛吃,可以吃多少天?
解析:此題就是典型的牛吃草問(wèn)題,在題目中,原有一片草場(chǎng)就是一個(gè)原始量,草勻速生長(cháng)對應的原始量的增加,牛吃草對應的原始量的減少,我們用線(xiàn)段AB來(lái)表示草場(chǎng),用一幅圖來(lái)分析一下牛吃草的規律。
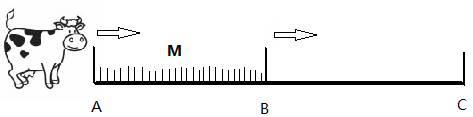
假設牧場(chǎng)原有草量是M(即AB段長(cháng)),牛從最左端A處開(kāi)始向右吃草,草從B段開(kāi)始向右生長(cháng),經(jīng)過(guò)T天后,在C處草被吃完了。相當于草從B點(diǎn)到C點(diǎn),同時(shí)牛從A點(diǎn)到C點(diǎn),很明顯與行程問(wèn)題中的追及問(wèn)題模型是一樣的。因此我們可以用追及公式來(lái)解決牛吃草問(wèn)題。假設每頭牛每天吃1份草,N頭牛每天就吃N份草;假設草每天生長(cháng)X份,則我們可以得出牛吃草的追及公式:M=(N - X)×T。然后將題干中的數據代入可得:(10 - X)×12=(15 - X)×6=(20 - X)×T,解得X為5,T為4。即對于20頭牛,4天就吃完了牧場(chǎng)上的草。
從這個(gè)問(wèn)題我們就可以總結牛吃草問(wèn)題的一個(gè)重要模型,即有一個(gè)原始量,對該原始量進(jìn)行一增一減兩個(gè)操作,這樣的問(wèn)題就可以看作牛吃草問(wèn)題,解題方法就是利用追擊公式,列出(牛速-草速)×時(shí)間= 原始量,代入數據求解即可。
接下來(lái)我們看能否利用這個(gè)模型和公式來(lái)套用其他的題目。
例2:一個(gè)水庫在年降水量不變的情況下,能夠維持全市12萬(wàn)人20年的用水量。在該市新遷入3萬(wàn)人之后,該水庫只夠維持15年的用水量。市政府號召節約用水,希望能將水庫的使用壽命提高到30年。那么該市市民平均需要節約多少比例的水才能實(shí)現政府制定的目標?
A.2/5 B.2/7 C.1/3 D.1/4
解析:由題干可知,水庫內原有水量是原始量,降水是對原始量的增加,居民用水是對原始量的減少,符合牛吃草問(wèn)題的基本模型。年降水量相當于草生長(cháng)速率,人數就相當于牛頭數。則可設年降水量為x,每萬(wàn)人每年原用水量為1,節水后每萬(wàn)人每年用水量為y,則可列出等式(12-x)×20=(12+3-x)×15=〔15y-x〕×30=初始水庫中水量,解得y=3/5,則節水比例為2/5,所以A為正確選項。
例3.某河段中的沉積河沙可供80人連續開(kāi)采6個(gè)月或60人連續開(kāi)采10個(gè)月。如果要保證該河段河沙不被開(kāi)采枯竭,問(wèn)最多可供多少人進(jìn)行連續不間斷的開(kāi)采?(假定該河段河沙沉積的速度相對穩定)
A.25 B.30 C.35 D.40
解析:由題干可知,原有河沙為原始量,沉積是對原始量的增加,開(kāi)采是對原始量的減少,符合牛吃草問(wèn)題的基本模型。沉積速度相當于草生長(cháng)速度,開(kāi)采人數相當于牛的頭數,直接利用公式:(80-x)×6=(60-x)×10,x=30,所以答案選擇B項。
更多解題思路和解題技巧,可參看2018年公務(wù)員考試技巧手冊。










