利潤問(wèn)題是行測考試中數量關(guān)系部分的一種題型，這種題型中有一類(lèi)考點(diǎn)，即求利潤的最值，此類(lèi)題目在求解過(guò)程中往往會(huì )出現一元二次函數，如何簡(jiǎn)便快速地求解一元二次函數的極值，下面小編就為大家介紹一種方法，即利用均值不等式來(lái)求解。
均值不等式的一種表達形式如下，
如果a、b均為非負實(shí)數，那么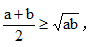
當且僅當a=b時(shí)，等號成立。
由上述表達式，我們可以得到如下結論：已知a、b均為正數，若a+b為定值，則當且僅當a=b時(shí)，ab取得最大值。
【例1】某商場(chǎng)銷(xiāo)售一批名牌襯衫平均每天可售出20件，每件盈利40元。為了擴大銷(xiāo)售增加盈利盡快減少庫存，商場(chǎng)決定采取適當的降價(jià)措施，經(jīng)調查發(fā)現如果每件襯衫每降價(jià)1元，商場(chǎng)平均每天可多售出2件，每件襯衫降低（ ）元時(shí)，商場(chǎng)每天盈利最多。
A.12
B.15
C.20
D.25
答案：B
接下來(lái)通過(guò)本題的解析我們梳理此類(lèi)題目的解題思路：
(1)找等量關(guān)系，列方程。
本題所求為利潤最值問(wèn)題，結合條件可以得出等量關(guān)系：總利潤=單件利潤×銷(xiāo)量。分析可得如果售價(jià)下降1元在成本不變的情況下利潤即下降1元，同時(shí)銷(xiāo)量會(huì )增加2件，這道題可以設每件襯衫的售價(jià)下降了x元，商場(chǎng)的總利潤為y元，那么可列出方程y=(40-x)×(20+2x)。
(2)湊配定和，求極值。
y=(40-x)×(20+2x)，由前面學(xué)習的均值不等式的結論可知，要想求兩部分乘積的最大值，需要這兩部分的加和為定值，而我們會(huì )發(fā)現40-x和20+2x的加和并不是常數，所以不為定值，那么就需要未知數在加和后抵消掉，則可將方程變形為y=2×(40-x)×(10+x)，此時(shí)40-x與10+x的和為定值，所以當且僅當40-x=10+x，即x=15時(shí)，y存在最大值，答案為B。
【例2】某賓館有50個(gè)房間供游客居住，當每個(gè)房間定價(jià)為每天180元時(shí)，房間會(huì )全部住滿(mǎn)，當每個(gè)房間的定價(jià)每增加10元時(shí)，就會(huì )有一個(gè)房間空閑，問(wèn)房?jì)r(jià)為多少元時(shí)賓館利潤最大？
A.260
B.280
C.300
D.340
答案：D
【解析】總收入最多則利潤最大，所以需要求出總收入的最大值，通過(guò)題干條件可得等量關(guān)系為：總收入=房間單價(jià)×入住房間數量，房?jì)r(jià)增加會(huì )使入住房間數減少，此時(shí)可設房?jì)r(jià)增加了x個(gè)10元，總收入為y元，可得y=(180+10x)×(50-x)，想求兩個(gè)部分乘積的最大值，需要使兩部分加和為定值，可將方程變形為y=10×(18+x)×(50-x)，當且僅當18+x=50-x，即x=16時(shí)，y取最大值，此時(shí)每個(gè)房間的價(jià)格為180+10×16=340元，故答案為D。
