數量
3種方法巧解不定方程題-2024山東公務(wù)員考試行測解題技巧
http://www.cqfhp.com/ 2023-06-07 來(lái)源：江蘇公務(wù)員考試網(wǎng)
方程法是解決行測數量關(guān)系題目的重要方法之一，對大多數考生而言，解普通方程難度不大，但是求解不定方程，除了最基本的代入排除之外，還能如何更快、更準確地解出正確答案呢？今天小編就帶大家來(lái)了解一下：
一、不定方程的定義
當未知數的個(gè)數大于獨立方程的個(gè)數時(shí)，我們稱(chēng)這樣的方程為不定方程。在實(shí)數范圍內，不定方程的解會(huì )有無(wú)數組，是不固定的。
二、正整數范圍內求解不定方程
解不定方程時(shí)根據未知數的取值特點(diǎn)進(jìn)行討論，會(huì )大大減少討論的次數，所以根據不定方程的特點(diǎn)，常用的解不定方程的方法除代入排除外，還可結合整除、奇偶性和尾數法等多種方法求解。
1.看到系數和常數有公約數，優(yōu)先想整除
【例1】小張的孩子出生的月份乘以29，出生的日期乘以24，所得的兩個(gè)乘積加起來(lái)剛好等于900，問(wèn)孩子出生在哪一個(gè)季度？
A.第一季度
B.第二季度
C.第三季度
D.第四季度
答案：D
【解析】設出生月份為x，出生日期為y，月份和日期都是正整數，則29x+24y=900，問(wèn)題為出生的哪一季度，需要知道小張孩子出生的月份，即x的值。由于24、900有公約數12，即都是12的倍數，所以29x也應是12的倍數，且29并不是12的倍數，則x應是12的倍數，即出生月份為12月，也就是第四季度。選擇D選項。
方法總結：在不定方程中，當其中一項未知數的系數與常數項有除1外的公約數時(shí)，可結合整除特性分析排除錯誤選項。
2.系數有奇有偶，方程不用愁
【例2】某單位向希望工程捐款。其中部門(mén)領(lǐng)導每人捐50元，普通員工每人捐20元，部門(mén)所有人共捐款320元，已知該部門(mén)總人數超過(guò)10人，問(wèn)該部門(mén)可能有幾名部門(mén)領(lǐng)導?
A.1
B.2
C.3
D.4
答案：B
【解析】設領(lǐng)導有x人，普通員工y人，人數必須為正整數，則50x+20y=320，化簡(jiǎn)得5x+2y=32。32和2y是偶數，則 5x必然是偶數，x為偶數，排除A、C。若領(lǐng)導有4人，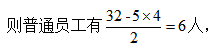
總人數沒(méi)有超過(guò)10，若領(lǐng)導有2人，
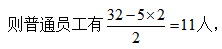總人數超過(guò)10人，故領(lǐng)導為2人，答案選B。
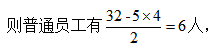總人數沒(méi)有超過(guò)10，若領(lǐng)導有2人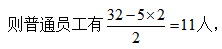，總人數超過(guò)10人，故領(lǐng)導為2人，答案選B。 方法總結：在不定方程中，當未知數的系數為一奇一偶時(shí)，可結合奇偶性分析，排除錯誤選項。
3.系數是5的倍數，尾數來(lái)幫你
【例3】現有451個(gè)同樣大小的橙子裝入大、小兩種袋子中，已知大袋每袋裝20個(gè)橙子，小袋每袋裝17個(gè)橙子，每個(gè)袋子都必須裝滿(mǎn)，問(wèn)至少需要小袋子的個(gè)數：
A.5
B.3
C.13
D.9
答案：B
【解析】設大袋子有x個(gè)，小袋子有y個(gè)，根據題意小袋子、大袋子共裝了451個(gè)橙子，可列方程 20x+17y=451。由于x、y 均為整數，20x的尾數一定為0，則17y的尾數必為 1，排除 A、D，代入B符合題意。
方法總結：當不定方程的解有正整數范圍限制時(shí)，若未知數的系數是5的倍數，那么該項的尾數就是0或5，就可以結合常數項的尾數將另外一項的尾數確定，進(jìn)而排除錯誤選項。
免費學(xué)習資源（關(guān)注可獲取最新開(kāi)課信息）
