“一筆畫(huà)最短距離”,是近年來(lái)行測考試中出現的新題型。由于這一類(lèi)題將幾何問(wèn)題與圖形推理中的一筆畫(huà)問(wèn)題相結合,比較新穎,很多考生對此束手無(wú)策,尤其是第一次遇到的同學(xué),就算能得出正確答案,也要耗費大量時(shí)間。今天江蘇公務(wù)員考試網(wǎng)(www.cqfhp.com)講解一下如何用一筆畫(huà)來(lái)解題,希望給考生一些幫助。
先讀題:
一塊由兩個(gè)正三角形拼成的菱形土地ABCD周長(cháng)為800米,土地周?chē)椭虚g的道路如下圖所示,其中DE、BF分別與AB和CD垂直。如要從該土地上任何一點(diǎn)出發(fā)走完每一段道路,問(wèn)需要行進(jìn)的距離最少是多少米?
A.1000+400√3
B.1100+400√3
C.1100+500√3
D.1000+600√3
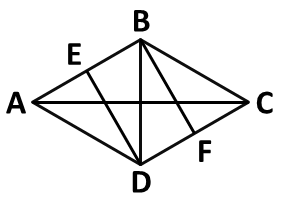
因為題干中要求必須走完每一條道路,那么,如果能夠按照一筆畫(huà)圖形不走重復路線(xiàn)的話(huà),行進(jìn)距離肯定是最短的。
我們先回顧以下一筆畫(huà)的相關(guān)知識:
1. 當奇點(diǎn)的個(gè)數為0或者2時(shí),這個(gè)圖形可以一筆畫(huà)完成。
2. 當奇點(diǎn)的個(gè)數為0時(shí),所有的點(diǎn)都是偶點(diǎn),可以從任意點(diǎn)出發(fā),完成一筆畫(huà)并且回到原點(diǎn)。
3. 當奇點(diǎn)的個(gè)數為2時(shí),必須從奇點(diǎn)出發(fā),回到另外一個(gè)奇點(diǎn),才能完成一筆畫(huà)。
我們觀(guān)察題中的圖形,圖中一共有4個(gè)奇點(diǎn),分別是A、E、F、C,至少需要兩筆畫(huà)完成,為了方便確定最短路線(xiàn),我們要想辦法讓它變?yōu)橐还P畫(huà)。
怎么變呢?可以將某些奇點(diǎn)連接起來(lái),讓這些奇點(diǎn)變?yōu)榕键c(diǎn),最終將圖形中的奇點(diǎn)數變?yōu)?或2。
如下圖所示,將圖1的兩個(gè)奇點(diǎn)連接,圖形就轉換成一筆畫(huà)圖形(圖2)。
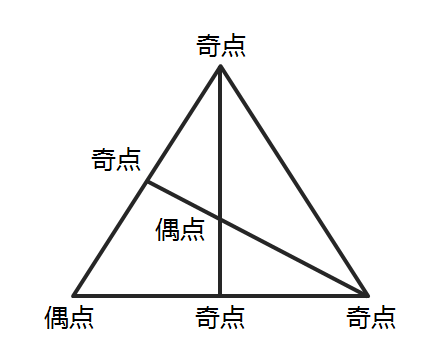
圖1
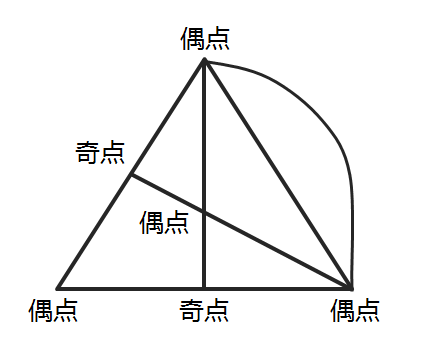
圖2
難點(diǎn)就在于這條連接線(xiàn)的長(cháng)度是多少呢?既然這條連接曲線(xiàn)是自行假設的,為了讓它盡可能短,根據“兩點(diǎn)之間線(xiàn)段最短”,不妨假設這條連接線(xiàn)的長(cháng)度就是原來(lái)兩個(gè)奇點(diǎn)的連接線(xiàn)(假設兩點(diǎn)為A、B,連接線(xiàn)長(cháng)度就是AB),就相當于這條線(xiàn)段走2次。
這樣,圖1就變成了一筆畫(huà)圖形,圖中所有路段都可以一筆走完。但要使得總路程最短,就應該選擇相鄰最近的兩個(gè)奇點(diǎn)變成偶點(diǎn)(假設兩點(diǎn)為B、C),如圖3,行走的最短距離=圖1中原有線(xiàn)段的長(cháng)度之和+BC。
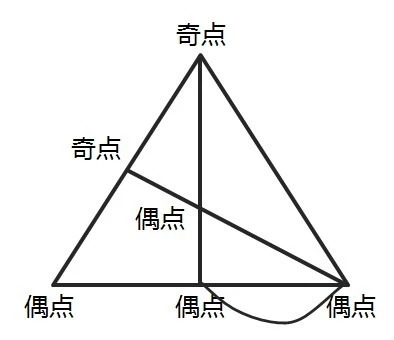
圖3
回到題目,觀(guān)察可知連接兩個(gè)奇點(diǎn)最短的距離是AE或者CF,為100米,則最短路程就是所有線(xiàn)段之和再加上AE或者CF的距離,S=800+200(BD的長(cháng))+4×100√3(4條正三角形的高)+100(多走的AE)=1100+400√3,正確答案為B。










